Two years ago I went to Atlanta to attend the “Gathering for Gardner,” a biennial conference on math, magic, games, and puzzles in honor of the late Martin Gardner. I gave an 8-minute talk at the meeting, and the video of my talk has just been posted online. Here it is!
If for any reason the embedded link doesn’t work, you can go to YouTube to watch it there.
The talk, called “Sun Bin’s Legacy,” is about a game I invented, called One-Round War, aka the World’s Simplest Card Game. Unfortunately, in the video you can’t see the lower part of the projection screen, so you can’t see my cards. To remedy that problem, I will show a couple of screen shots below.
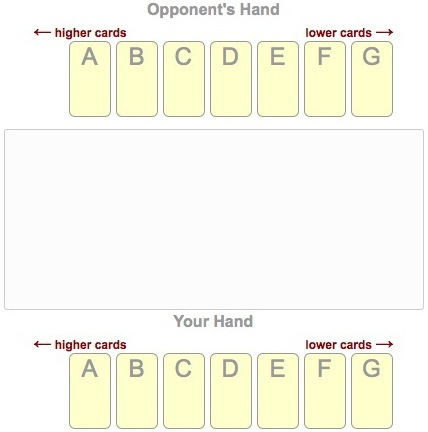
One-Round War is played with a deck with an even number of cards. (For illustration, let’s say 14. In general, the number of cards would be 2n.) There is only one suit, and the cards are labeled from 1 to 14 with 14 being strongest. The cards are dealt face-down, half to one player and half to the other. The most important and distinctive rule is that the dealer places them in front of each player in order of strength. So even though you don’t know what cards you or your opponent has, you do know which card is his strongest, which is your strongest, etc. Here are the cards after dealing, with the strongest labeled A, the next B, and so on.
On each round of the game, Player 1 plays one card from his hand without turning it over, and Player 2 does likewise. After all cards are played, the players turn over their cards to reveal who won the tricks. The person with the most tricks wins the game. It’s called “One-Round War” because it’s similar to the children’s game of War, but simpler because you only go through the deck one time (and there are no ties because there is only one suit).
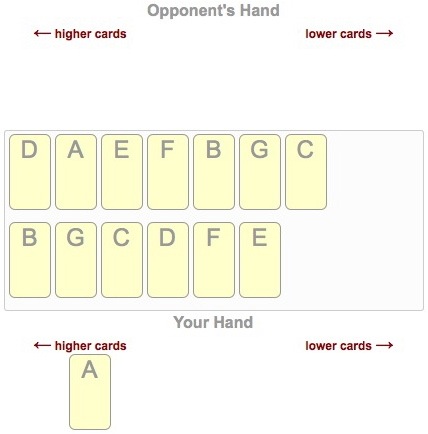
If I’m Player 2, here is how the game might look halfway through the last trick.
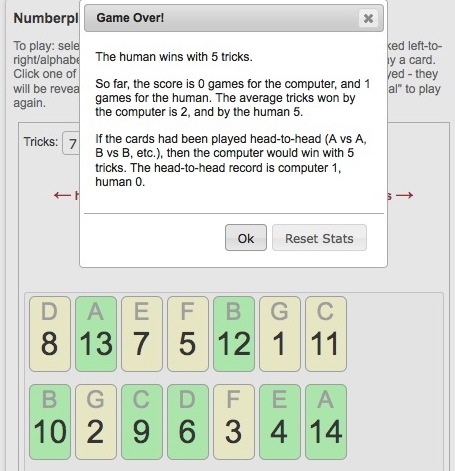
Here’s how to read this. On the first trick, the opponent played his card D and I played my card B against it. On the second trick, he played his card A (his best card) and I played my card G (my worst card) against it. And so on. Now, on the last trick, he has played C and I am about to play A, my only remaining card against it. After doing so, we turn over the cards to reveal who won the tricks.
As you can see, the opponent won only two tricks, the ones where I “sacrificed” my lowest cards (F and G) against his highest cards (A and B). I won the remaining five tricks. (Winning cards highlighted in green.) Note that if I had played the chump’s strategy, A versus A, B versus B and so on, I would have lost 5-2 instead of winning 5-2.
In my lecture I was only able to scratch the surface, so I’ll say a little bit more here about the optimal strategy. First, let me explain that I will define “optimal” as winning the most tricks on the average. (For example, if we’re betting $1 on each trick, this is the strategy I would want to use. If instead we are betting $1 on each game, the optimal strategy is different and much easier — see the lecture.)
Optimal strategy for One-Round War:
- Separate your cards into two groups: the sacrificial cards (here, F and G) and the strong cards (here, A through E).
- Play your sacrificial cards against his best cards in reverse order of strength. (Thus, I played my two weakest cards, F and G, against his two strongest, A and B, with G going against A and F against B.)
- Play your strong cards against his weakest cards in normal order of strength. (Thus, I played A against C, B against D, C against E, etc.)
- Finally, the key question is: How many cards should you sacrifice? Why did I decide to sacrifice two, as opposed to one or three?
The rule for determining the number of sacrificial cards is absolutely amazing. I could not believe it when I discovered it, but I have proved mathematically that it gives you the highest expected winnings. First, I write down Pascal’s triangle.
If I’m playing with 14 cards, I go to the 14-th row of the triangle and I start adding the numbers left to right. (In general, if there are 2n cards, I would go to the 2n-th row.) I stop when the sum first becomes greater than the center number in that row.
The 14th row goes as follows: 1, 14, 91, 364, 1001, 2002, 3003, 3432, 3003, … The center element of the row is 3432. Adding from left to right, I get
1 + 14 + 91 + 364 + 1001 + 2002 = 3473 > 3432.
I stop here because the sum is greater than the central element. Finally, I count how many steps it takes to get from the last element I added (2002) to the central element (3432). The answer is two places, and that is the number of cards I need to sacrifice.
All I can say is: MATH IZ KEWL!
This all got turned into an article that appeared in the September 2015 issue of College Mathematics Journal, in case you want to read more details.
Unfortunately I don’t think that this game will ever catch on because you either need to play on a computer or else you need a fairly intelligent dealer who can be relied on to put the cards face-down in order of strength. However, if it weren’t for the implementation issue, I think it would be a great game for hustlers, because it seems at first sight like a fair game. None of the cards are turned over during play, so there is no way for the hustler to know what cards he has or what cards the mark has. So how can the hustler possibly have an advantage? The secret, of course, is that he has more information — he always knows his opponent’s move. (But when he is explaining the game to the mark, he should pretend that he is being generous by letting the mark go first.)
It’s possible that some marks could catch on to the fact that moving first is a disadvantage. Even then, the hustler could offer to play half of the games as player two and half as player one. Because the mark would not know the optimal strategy, and would not know the correct number of cards to sacrifice, it is likely that the hustler could still make money. (Just not as much.)
Okay! You’ve just spent more time reading my post than watching the lecture. Actually, I hope you enjoyed both. Sorry that there isn’t any chess in this post, except for the word “sacrifice.”
Addendum: In the lecture I said that my proof of the optimal strategy was only valid if n is greater than 10 million, i.e., each player has 10 million cards or more in their hands. This somewhat limited the practicality of the result! However, I subsequently teamed up with another mathematician named Richard Chatwin, who improved my proof to such an extent that it worked for n greater than 40. He also verified the remaining cases (n = 3 to 40) by computer. Thus we have completely solved the problem of finding the best strategy, no matter how many cards are in the deck.